導入
前章では、静止流体が及ぼす力に関する正確な数学的状況は容易に得られることを示しました。これは、静水力学では単純な圧力のみが関与するからです。運動する流体を考慮すると、解析の問題は一挙にはるかに困難になります。粒子速度の大きさと方向を考慮する必要があるだけでなく、運動する流体粒子間および粒子境界においてせん断応力または摩擦応力を引き起こす粘性の複雑な影響も考慮する必要があります。流体体の異なる要素間の相対運動により、圧力とせん断応力は流れの状態に応じて点ごとに大きく変化します。流動現象に伴う複雑さのため、正確な数学的解析はごく限られたケースでしか不可能であり、工学的観点からはやや非現実的です。したがって、流動の問題は、実験によって、あるいは理論的解を得るのに十分な単純化のための仮定を置くことによって解く必要があります。この2つのアプローチは相互に排他的ではありません。なぜなら、力学の基本法則は常に有効であり、いくつかの重要なケースでは部分的に理論的な手法を採用することができるからです。また、単純化された分析の結果としての真の条件からの逸脱の程度を実験的に確認することも重要です。
最も一般的な単純化の仮定は、流体が理想的あるいは完全であるという仮定であり、複雑な粘性効果を排除するものである。これは、ストークス、レイリー、ランキン、ケルビン、ラムといった著名な学者たちが注目してきた応用数学の一分野である古典流体力学の基礎である。古典理論には重大な固有の限界が存在するが、水の粘性は比較的低いため、多くの状況において実流体として挙動する。このため、古典流体力学は流体運動の特性を研究する上で最も貴重な背景知識とみなすことができる。本章は流体運動の基本的な力学を扱い、土木工学水理学で遭遇するより具体的な問題を扱う後続の章への基本的な導入となる。流体運動の重要な3つの基本方程式、すなわち連続方程式、ベルヌーイ方程式、および運動量方程式を導出し、その意義を説明する。その後、古典理論の限界を考察し、実流体の挙動について説明する。本章全体を通して非圧縮性流体を仮定する。
フローの種類
さまざまな種類の流体運動は、次のように分類できます。
1.乱流と層流
2.回転と非回転
3.安定と不安定
4.均一と不均一。
MVSシリーズ軸流ポンプ AVSシリーズ斜流ポンプ(垂直軸流ポンプおよび斜流水中汚水ポンプ)は、海外の最新技術を採用して設計された最新製品です。新型ポンプは、従来品より容量が20%増加し、効率は3~5%向上しています。

乱流と層流。
これらの用語は、流れの物理的性質を説明します。
乱流では、流体粒子の進行は不規則で、一見無秩序な位置交換が見られます。個々の粒子は変動する横方向速度の影響を受けるため、運動は直線的ではなく、渦を巻くように蛇行します。染料を特定の地点に注入すると、流れ全体に急速に拡散します。例えば、パイプ内の乱流の場合、ある断面における速度の瞬間的な記録は、図1(a)に示すような近似分布を示します。通常の計測機器で記録される定常速度は点線で示されており、乱流は時間的に定常な平均速度に非定常な変動速度が重畳した特徴を持つことがわかります。
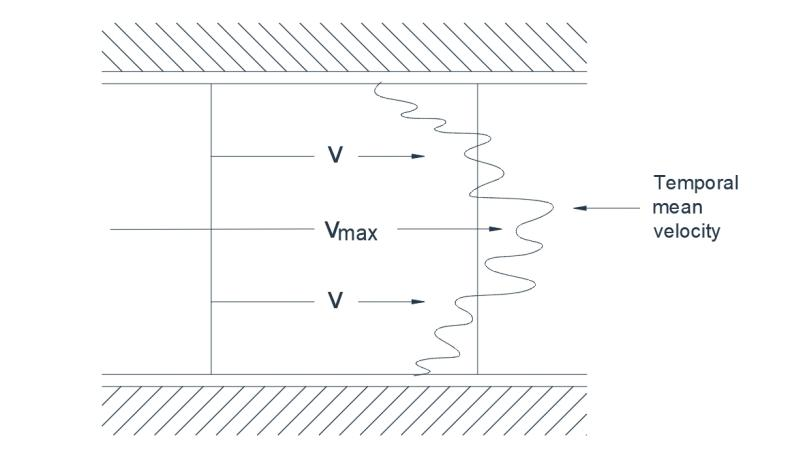
図1(a) 乱流
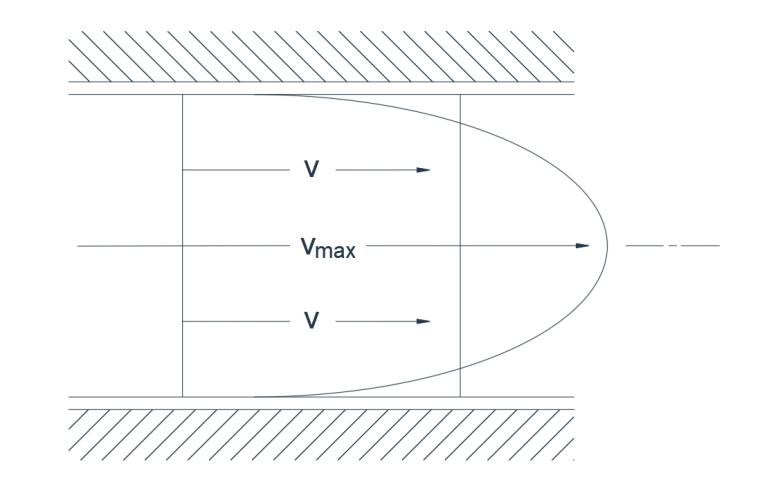
図1(b) 層流
層流では、すべての流体粒子は平行な経路に沿って進み、速度の横方向成分は存在しません。各粒子は、前の粒子の経路を逸脱することなく正確にたどり、規則的に移動していきます。したがって、細い染料の糸は拡散することなくそのままの状態を保ちます。層流(図1b)では、乱流よりも横方向の速度勾配がはるかに大きくなります。例えば、パイプの場合、平均速度Vと最大速度V max の比は、乱流では0.5ですが、層流では0.05です。
層流は、低速かつ粘性があり動きの遅い流体と関連しています。パイプラインや開水路の水理学では、固体境界近傍に薄い層流層が残存する場合でも、ほぼ常に十分に高い速度で乱流が発生します。層流の法則は十分に理解されており、単純な境界条件であれば速度分布を数学的に解析できます。しかし、乱流は不規則な脈動特性を持つため、厳密な数学的処理が困難であり、実用的な問題の解決には、主に経験的または半経験的な関係に頼る必要があります。

型番:XBC-VTP
XBC-VTPシリーズ垂直長軸消火ポンプは、最新の国家規格GB6245-2006に準拠して製造された単段・多段ディフューザーポンプです。米国防火協会(USAF)の規格を参考に設計を改良しました。主に石油化学、天然ガス、発電所、綿織物、埠頭、航空、倉庫、高層ビルなどの産業における消火水供給に使用されます。また、船舶、海上タンク、消防船などの供給用途にも適用できます。
回転流と非回転流。
各流体粒子が自身の質量中心の周りで角速度を持っている場合、その流れは回転していると言われます。
図2aは、直線境界を通過する乱流に伴う典型的な速度分布を示しています。不均一な速度分布のため、本来2つの軸が直交する粒子は、わずかな回転角で変形します。図2aでは、円形の流れが
速度が半径に正比例する経路が描かれています。粒子の2つの軸は同じ方向に回転するため、流れは再び回転します。
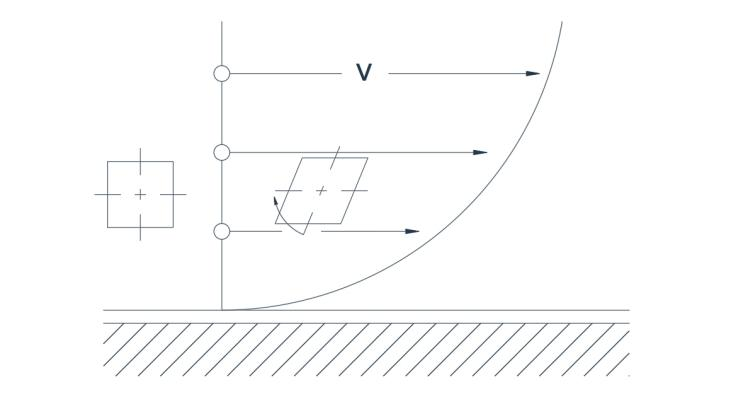
図2(a) 回転流
流れが非回転であるためには、直線境界に隣接する速度分布が均一でなければなりません(図2b)。円軌道内の流れの場合、非回転流れは速度が半径に反比例する場合にのみ成立することが示されます。図3を一見すると、これは誤りのように見えますが、詳しく見ると、2つの軸が反対方向に回転するため、補償効果が生じ、軸の平均方向は初期状態から変化しないことがわかります。
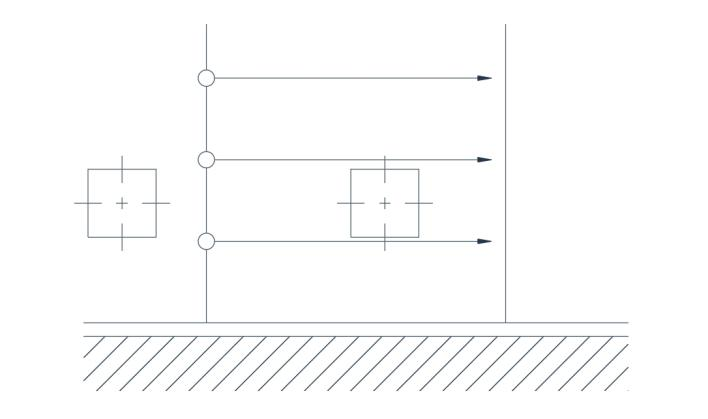
図2(b) 非回転流れ
すべての流体は粘性を持つため、現実の流体の流速は真の非回転流には決してならず、層流は当然ながら強い回転性を持っています。したがって、非回転流は仮説的な状態であり、乱流の多くの例において回転特性が極めて小さいため無視できるという事実がなければ、学術的に興味深いものとなるでしょう。これは、前述の古典流体力学の数学的概念を用いて非回転流を解析できるため、便利です。
型番:ASN ASNV
モデル ASN および ASNV ポンプは、単段両吸込分割渦巻ケーシング遠心ポンプであり、水道、空調循環、ビル、灌漑、排水ポンプ場、発電所、工業用給水システム、消防システム、船舶、ビルなどの液体輸送に使用されます。

安定した流れと不安定な流れ。
流れが定常であると言われるのは、どの点においても状態が時間的に一定である場合です。この定義を厳密に解釈すると、乱流は真に定常であるはずがないという結論に至ります。しかし、ここでは流体の一般的な運動を基準とし、乱流に伴う不規則な変動は副次的な影響に過ぎないと見なすのが便宜です。定常流の分かりやすい例としては、導管や開水路における一定流量の流れが挙げられます。
結果として、時間経過とともに条件が変化すると、流れは非定常となる。非定常流の例としては、導管や開水路における流量の変動が挙げられる。これは通常、定常流量に続く、あるいは定常流量に続く過渡現象である。その他のよく知られた現象としては、
より周期的な性質の例としては、波の動きや潮流における大きな水体の周期的な動きが挙げられます。
水理工学における実際的な問題のほとんどは定常流に関するものです。これは幸運なことです。なぜなら、非定常流では時間変数が解析を著しく複雑にするからです。したがって、本章では、非定常流の考察は比較的単純ないくつかのケースに限定します。ただし、一般的な非定常流の例のいくつかは、相対運動の原理によって定常状態にまで簡略化できることを念頭に置くことが重要です。
このように、静水面を航行する船舶に関する問題は、船舶は静止し、水は動いているという形で言い換えることができる。流体挙動の相似性に関する唯一の基準は、相対速度が同じであることである。また、深海における波動は次のように簡約できる。
観測者が波と同じ速度で移動すると仮定して定常状態を実現します。

ディーゼルエンジン式垂直タービン多段遠心インラインシャフト排水ポンプ このタイプの垂直排水ポンプは、主に腐食がなく、温度が60℃未満、浮遊物質(繊維質、砂利などを除く)含有量が150mg/L未満の汚水または廃水の汲み上げに使用されます。VTP型垂直排水ポンプはVTP型垂直給水ポンプの一種で、増圧と給油をベースとし、給油チューブに水潤滑油をセットします。60℃以下の温度で、特定の固形物(例えば、鉄くず、細砂、石炭など)を含む汚水または廃水を汲み上げることができます。
均一な流れと不均一な流れ。
流れが一様であるとは、流れの経路上のある点から別の点まで、速度ベクトルの大きさと方向に変化がないことを意味します。この定義に従うためには、流れの面積と速度は、すべての断面において同じでなければなりません。不均一な流れは、速度ベクトルが場所によって変化する場合に発生し、典型的な例としては、収束境界または発散境界間の流れが挙げられます。
これら2つの代替的な流れ条件は、開水路水理学では一般的ですが、厳密に言えば、一様流は常に漸近的に近づくため、それは近似値をとるだけで実際には到達できない理想的な状態です。これらの条件は時間ではなく空間に関連するため、密閉された流れ(例えば、圧力がかかっているパイプ)の場合、流れの定常性または非定常性とは全く無関係であることに留意する必要があります。
投稿日時: 2024年3月29日
 sales@tkflow.com
sales@tkflow.com 
